Impedance Triangle is a right angle triangle whose sides represent the impedance. The base, perpendicular and hypotenuse represents Resistance, Reactance and Impedance respectively. It is basically a geometrical representation of circuit impedance.
Using impedance triangle we can find the resistance if the impedance and reactance is known.
What is impedance Triangle?
Impedance (Z) consists of two components
- Resistance( R)
- Reactance (X)
Resistance draws the real power or active power because phase angle between voltage and current is zero. The base of the right angle represents the active power, and therefore the base of the triangle represents resistance(R)
Reactance(X) is the reactive component which draws reactive power. The net active power drawn by reactance is zero. In half cycle it draws the reactive power and in other half cycle it again deliver reactive power to mains supply. The angle between the voltage & current is 90 degree and active power drawn by reactive power is zero.
Thus, we can represent the reactive component(X) on the perpendicular side of the triangle.
From above it is clear that resistance(R) and reactance(X) are 90 degree to each other on a impedance triangle. The impedance is the combination of the resistance(R) and reactance(X). SI units of resistance,reactance and impedance is ohm (Ω).
The impedance(Z) can be represented on the hypotenuse side of the triangle. Therfore, impedance(Z) is a complex number. We represent the complex number like A+jB.
The total opposition offered by a circuit to flow of an alternating current circuit is called impedance. The opposition is created by circuit components R,L & C.
Z = R + j X
Representation of R,X and Z on Impedance Triangle
The geometrical representation of R, X, and Z is shown below.
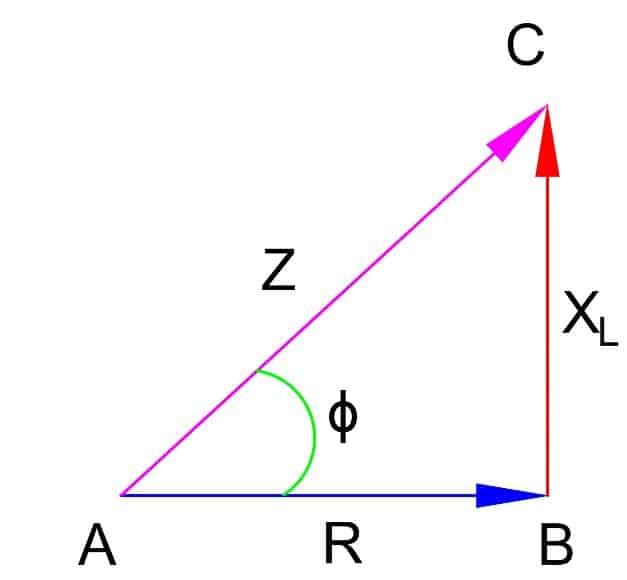
The above triangle ABC is called impedance triangle. Here.
AB = Base of triangle = R
BC = Perpendicular of triangle = X
AC = hypotenuse of triangle = Z
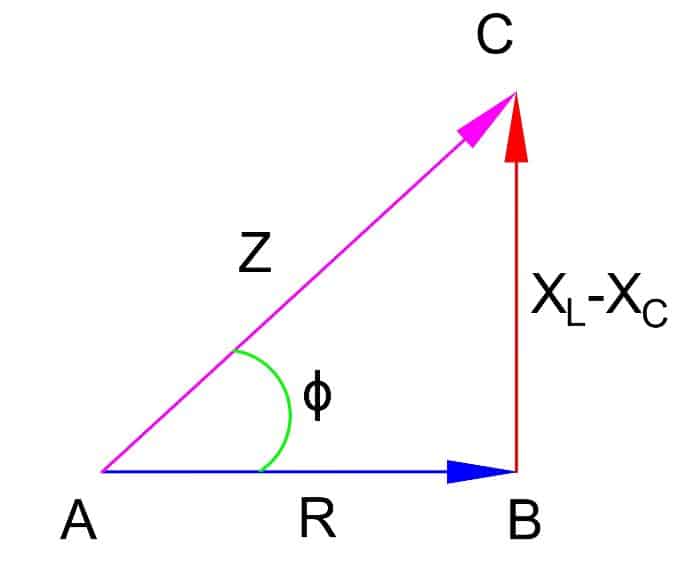
If the circuit has R,L & C components, then the capacitor and inductor both offer the reactance. The reactance of the inductor is in just phase opposition to the capacitor and net reactance in this case is;
X = XL – XC
Where, XL and XC are frequency dependent.
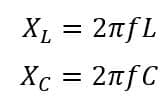
Relationship between R,L and C
We can establish the relationship between R,X and Z using Pythagoras Theorem for ringht angle triangle ABC.
AC2 = AB2 + BC2
Z2 = R2 + X2
Z = √ (R2 + X2 )
Impedance Triangle of RL,RC and RLC circuit
RL circuit impedance
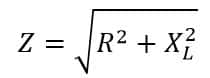

Impedance of RC circuit ;
Impedance of RLC circuit;
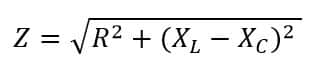
| Read More : Resistance & Leakage Reactance of Transformer |
The angle between resistance(R) and impedance(X)
tan ø = (X/R)
ø = tan-1(X/R)
Hence, using Impedance Triangle, we can find the magnitude and the angle of impedance of a circuit.
Significance of Impedance Triangle
We can find the following electrical quantities using impedance triangle.
- Impedance
- Power Factor
1. Calculation of Impedance
We can calculate the impedance of the complex circuit, if we have the known quantity data like resistance(R) and reactance(X).
Z = √ (R2 + X2 )
2. Calculation of Power Factor
cosø represents the power factor of the triangle. In traiongle ABC,
Cosø = AB/ AC = R /Z
Cosø = R / Z
Let the impedance of a circuit is Z = 10+j8. From these data we can calculate the impedance and power factor of the circuit.
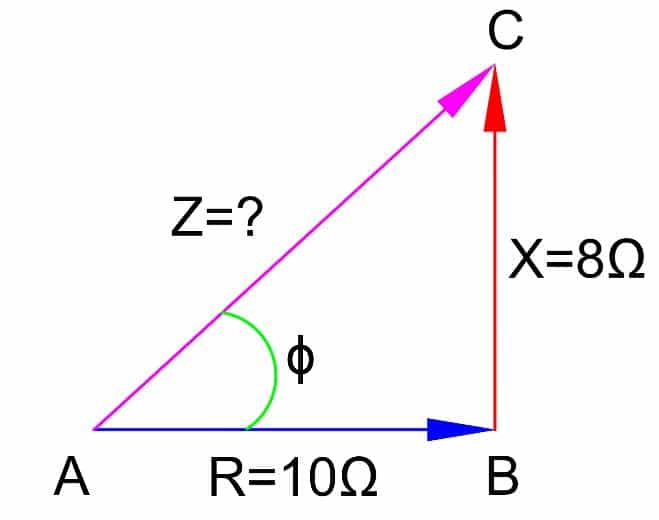
Z = √ (R2 + X2 )
Here, R = 10 Ω
X = 8 Ω
Z = √ (102 + 82 ) = √ (100 +64 ) = √ 164
= √ 164
Z = 12.8 Ω
Impedance of the circuit is 12.8 Ω .
Power Factor
Cosø = R / Z = 10/12.8
Cosø = 0.781
Read Next :