The ultracapacitors like conventional capacitors store electric energy in the form of an electrostatic field. However, an ideal ultracapacitor does not lose stored energy. Parallel plate capacitors are the simplest form of a capacitor that has two conductive parallel plates separated by a certain distance(d). In between the parallel plates, there exist insulating materials like air, mica, paper, oil, and ceramic, and these insulating materials are called dielectric materials.
The capacitor stores the electric energy in the form of charge. The charge-storing capacity of a capacitor depends on the voltage and the capacitance of the capacitor. The capacitance of a capacitor shows its charge-storing capacity. The higher capacitance value of a capacitor for the same voltage will cause it to store more charge because of Q ∝ C. In a similar manner, if the voltage is increased across the plates of the capacitor keeping the same capacitance, it will store more electric energy because of Q ∝ V.
Note: Never apply a voltage more than the rated voltage of the capacitor. It may cause damage to the capacitor.
Now, we can establish the relationship between Q, C, and V.

The capacitance of a capacitor is C= Q/V, therefore the unit of capacitance is the coulomb/volt. We can call Coulomb/volt as the Farad (F). When a charge of 1 coulomb cause a 1-volt potential difference between the plates, then the capacitance of a capacitor is 1 Farad. The smaller units of capacitance are microfarad (μF), nano-farad (nF), and picofarad (pF) are commonly used.
The relationship between different units of capacitance is given below.
| Capacitance Unit | Capacitance Value | Equivalent Farad |
| Millifarad (mF) | 1mF | 10-3 F |
| Microfarad (μF) | 1μF | 10-6 F |
| Nanofarad (nF) | 1nF | 10-9 F |
| Picofarad (pF) | 1pF | 10-12 F |
The ultracapacitors or supercapacitors are available in a very small size with a capacitance value in the range of milli-farad(mF) to ten’s farad. A capacitor that has a large value of capacitance can store more energy. The relationship between the charge and energy stored in the capacitor is given below.

From the above equation, it is clear that a capacitor that has a large capacitance value can store more electric energy in comparison to a capacitor with a small capacitance value. Now, we will see how we can increase the capacitance of a capacitor. The capacitance of a capacitor depends on the permittivity(ε), area of plates(A), and separation distance(d) between the plates. The capacitance of parallel plate capacitor is;

From the above equation, it is clear that if we increase the area (A) of plates, increase the permittivity of the medium(ε) & reduce the distance between the plates(d), we can get a larger capacitance that can store the more electrical energy. The same concept is used in ultracapacitors.
Thus, the ultracapacitor or supercapacitor has a large conductive plate surface area(A) and a small distance (d) between the conducting plates. It also has a dielectric medium different from the conventional capacitor. The conventional capacitor has solid and dry dielectric materials such as Polyethylene, paper, mica, Teflon, etc. On the other hand, ultracapacitors have wet or liquid dielectric between the plates and thus these capacitors have a large permittivity in comparison to conventional capacitors.
The ultracapacitors store the electric energy in the form of an electric field similar to the conventional capacitors. However, ultracapacitors can store large electric energy because they have a larger capacitance.
Construction of Ultracapacitors
An Ultracapacitors Construction is shown in the below picture.
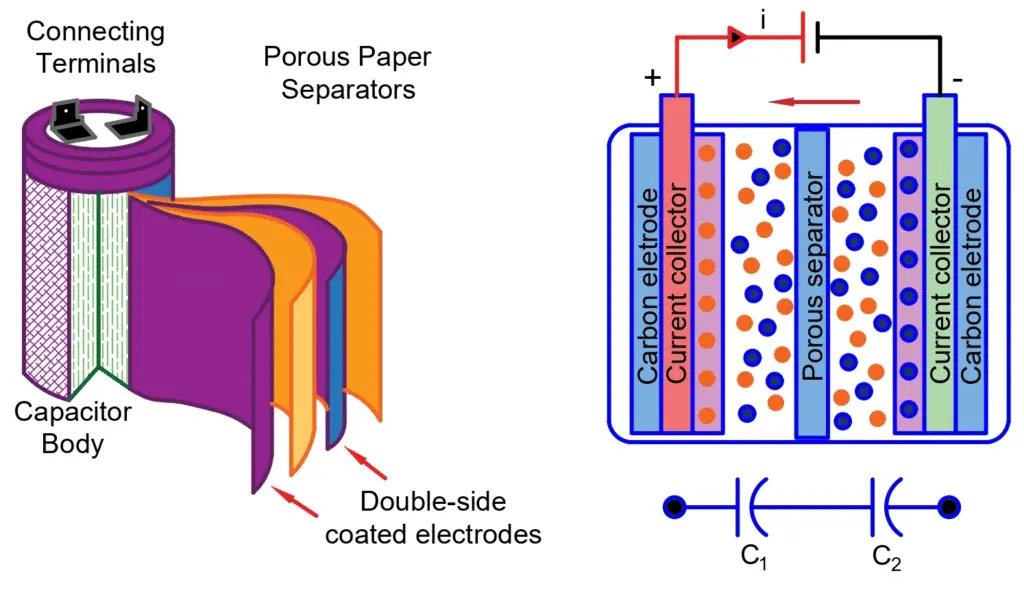
The double-sided coated electrodes have graphite carbon in the form of activated conductive carbon, carbon nanotubes, or carbon gels. It has a separator made of porous paper that allows the positive ions to pass through while blocking the larger electrons. The paper separator and carbon electrodes are then impregnated with liquid electrolyte with an aluminum foil.
Although the double-layered carbon electrodes and separator are very thin, the effective surface area is thousand of meters squared after coiling them together. That is why, ultracapacitors have a larger capacitance and they have a larger capacity to store electrical energy even being compact in size.
Ultracapacitors are excellent energy storage devices because they have high capacitance value, in the order of hundreds of farad. The double-layered construction of the ultracapacitors forms two capacitors, one at each carbon electrode. Therefore, ultracapacitors are also called double-layer capacitor that forms two capacitors in a series.
The small size of the ultracapacitor creates one limitation of keeping the low voltage across the ultracapacitor’s cell because the voltage rating of the capacitor is determined by the decomposition voltage of the electrolyte. The capacitor cell voltage is typically in the range of 1 to 3 volts which is the limiting factor for the storage of electrical energy.
The solution to this problem is that the cells of the ultracapacitors are connected in series and parallel combinations to increase the storage capacity of electrical energy. Thus, when we connect the capacitors in the series and parallel combination the rated terminal voltage increases from 1 to 3 volts to tens of volts.
Increasing Ultracapacitors Value
The capacitance value of ultracapacitors can be increased by connecting the capacitors in parallel and series connections.
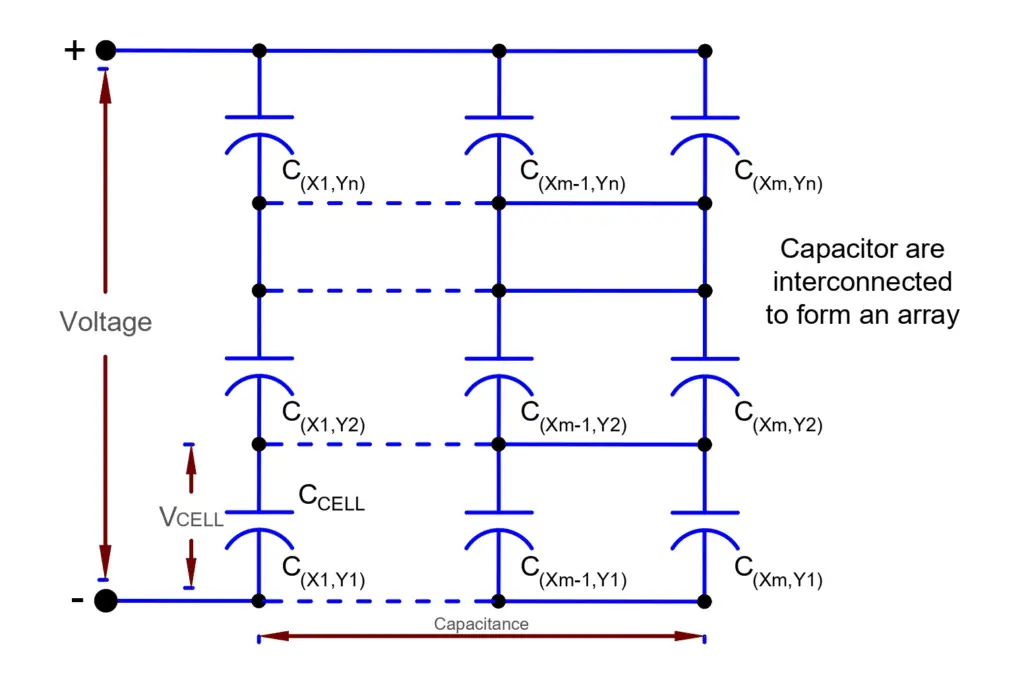
When we connect capacitors in parallel their capacitance value increases, and thus connecting capacitors in parallel we can get a larger capacitance value. As we know, the energy stored in the capacitor depends on the capacitance as well as voltage. The parallel connections of capacitors lead to increases the capacitance, but what needs to do for increasing voltage? We can increase the voltage by connecting the capacitors in the series.
The series and parallel connections of capacitors, thus, increase the capacitance as well as energy storage capacity.
Let,
P= Number of columns in the capacitor array
Q= Number of rows in the capacitor array
VCELL= Voltage of each cell
The total voltage appearing at the capacitor terminal is;
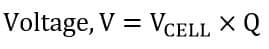
Total capacitance is;
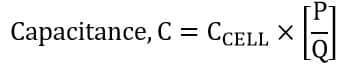
Note: Similar to batteries, ultracapacitors or supercapacitors have polarity with a positive terminal marked on the capacitor’s body.
Ultracapacitors Example No1
An electronic circuit requires a 6-volt, 3-farad ultracapacitor for energy storage backup. If the individual ultracapacitor rating is 3V, 1.0 F cells, calculate the number of cells required and the layout of the array.
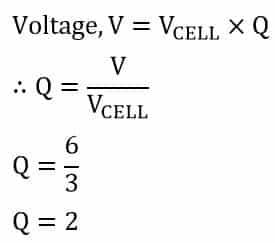
The array will therefore have two capacitor cells of 3 volts each connected in series and providing 6 volts.
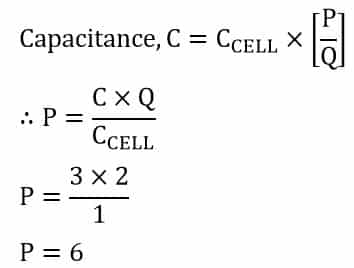
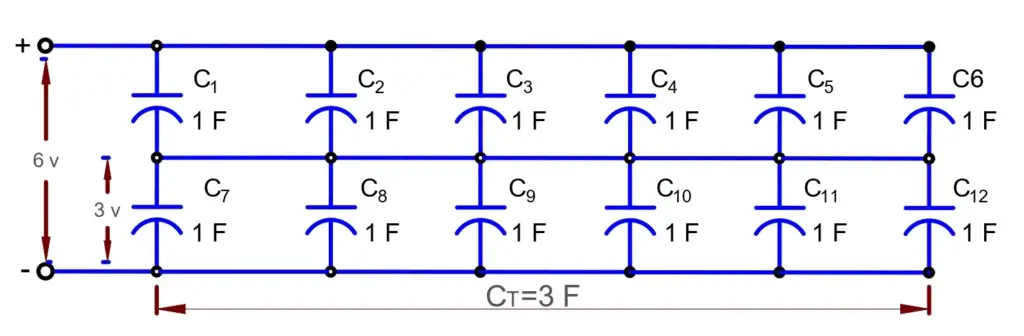
The array will have a total of six individual columns. Thus, the ultracapacitors have a 6 X 2 array as shown in the below picture.
Ultracapacitor Energy
Ultracapacitors like conventional capacitors store the energy as a charge in the electric field between the plates. There will always exist a potential difference between the plates when a capacitor holds charges. When a capacitor is charged with a voltage source V, the voltage across its terminal becomes equal to the supply voltage upon getting fully charged.
After fully charging of the capacitor, the charging current stops flowing. Now, if we remove the supply voltage, the capacitor terminal voltage will remain at the supply voltage potential.
When the capacitor is connected to an electrical load, it supplies electric power to the load and gradually its terminal voltage falls. When the capacitor gets fully discharged it can not supply current to load and now, we need to again recharge the ultracapacitor.
The energy stored in a capacitor is proportional to the capacitance C and the square of the voltage V across its terminal. Therefore, energy stored in a capacitor is;
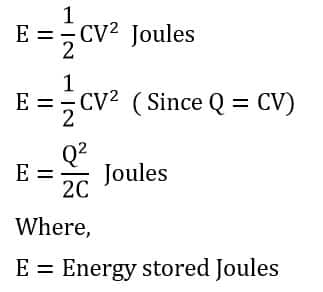
Energy stored in a capacitor taking our ultracapacitor example above,
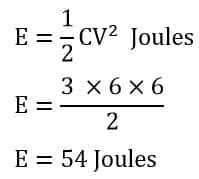
Thus, the ultracapacitor stores the 54 Joules energy when it is connected to 6 volts supply source. After charging the capacitor, the entire 54 joules of energy is available and when it is connected to the load it delivers this energy, and finally, on discharging the stored energy becomes zero.
Now, the capacitor is ready to take power from the external power source for charging and storing the energy. After charging, the stored energy can be delivered to the electrical load.
The ultracapacitor has a capacitance value in the order of thousands of farad and voltage in the order of hundreds of volts. Thus, the ultracapacitors are capable of storing large electric energy. A large electric energy storing feature of the ultracapacitors makes them suitable for applications like electric braking, E-vehicle, and renewable energy.