In modern power system engineering, unbalanced conditions are common due to asymmetrical faults, uneven loads, or line parameter differences. Analyzing such unbalanced systems directly can be complex and time-consuming. To simplify this, engineers use Symmetrical Components, a mathematical technique that transforms unbalanced three-phase phasors into three sets of balanced phasors.
This method provides a clear way to analyze, calculate, and protect power systems efficiently.
What Are Symmetrical Components?
Symmetrical Components are a set of three separate phasors that represent the balanced parts of an unbalanced three-phase system. Each set behaves like a balanced three-phase system, even if the original system is unbalanced.
The three sets are:
- Positive Sequence Components
- Represent the normal operating condition.
- All three phasors have equal magnitude and are displaced by 120° in the A-B-C sequence.
- Helps analyze the power flow under normal or slightly unbalanced conditions.
- Negative Sequence Components
- Phasors have equal magnitude but are displaced by 120° in reverse order (A-C-B).
- Generated during unbalanced faults, such as line-to-line faults.
- Can cause heating in generators and motors if not properly accounted for.
- Zero Sequence Components
- All three phasors are in phase with each other and equal in magnitude.
- Represents currents that flow through the neutral or ground.
- Often observed in line-to-ground faults.
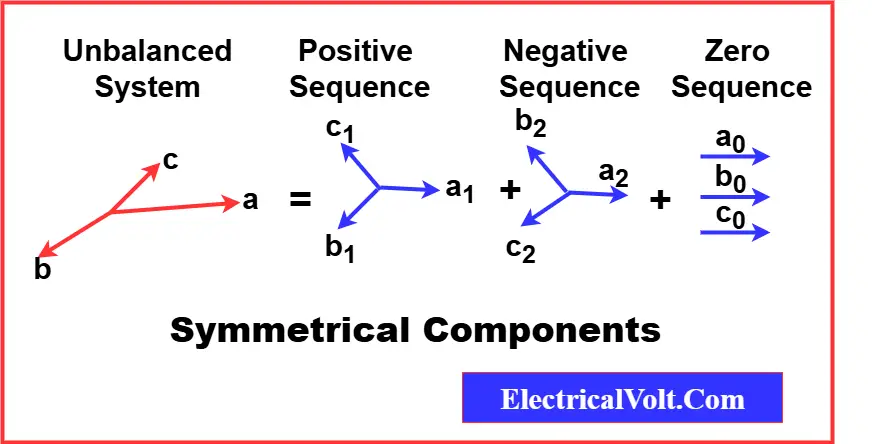
Symmetrical Components of Unbalanced Phasors
When a system becomes unbalanced, phase voltages (Va, Vb, Vc) or currents (Ia, Ib, Ic) differ in magnitude and phase angle. Using symmetrical components of unbalanced phasors, these unbalanced quantities can be mathematically separated into three balanced sets using the following symmetrical components formula.
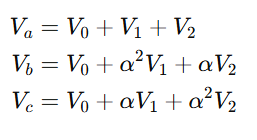
Where:
- V0 = Zero sequence component
- V1 = Positive sequence component
- V2 = Negative sequence component
- α=ej120∘=−1/2+j√3/2
This is the standard way to express unbalanced phasors using symmetrical components.
This transformation allows engineers to analyze each sequence separately, using simpler circuit models.
How Symmetrical Components Are Calculated
- Identify the unbalanced phasors: Measure or calculate the phase voltages or currents.
- Apply transformation equations: Convert the unbalanced set into positive, negative, and zero sequences using matrix methods.
- Analyze each sequence separately: Study fault currents, voltage drops, or load effects.
- Combine results if needed: Reconstruct the original unbalanced phasors from the three sequences for practical system evaluation.
This approach reduces a complex three-phase unbalanced problem into three simpler, balanced problems.
Applications of Symmetrical Components
Symmetrical Components are widely used in power system analysis and design:
- Fault Analysis:
Quickly analyze single line-to-ground, line-to-line, and three-phase faults. - Unbalanced Load Analysis:
Helps study voltage unbalance and current distribution in distribution networks. - Protection Relays:
Relays use positive, negative, and zero sequence components to detect and isolate faults efficiently. - Power Quality Studies:
Detects harmonics, voltage sags, and other disturbances caused by unbalanced loads. - Generator & Motor Protection:
Negative sequence components help prevent overheating and mechanical stress in rotating machines.
Advantages of Using Symmetrical Components
- Simplifies complex unbalanced systems into three manageable systems.
- Reduces mathematical complexity in fault calculations.
- Helps in protective relay coordination.
- Provides insight into neutral currents and system stability.
- Improves fault detection accuracy, enhancing power system safety.
Example: Fault Analysis Using Symmetrical Components
Consider a single line-to-ground fault on phase A. The unbalanced phase voltages can be decomposed into:
- Positive sequence voltage (V1) → normal operating component
- Negative sequence voltage (V2) → reverse phase component
- Zero sequence voltage (V0) → ground current component
By analyzing each sequence separately with per-sequence impedances, we can calculate the fault current and voltage drops accurately without solving the full unbalanced system directly.
Conclusion
Symmetrical Components are an essential tool in modern power system engineering. They simplify the analysis of unbalanced phasors, enhance fault detection, and improve system protection and reliability. Understanding symmetrical components is crucial for engineers working in power generation, transmission, and distribution systems.
With this approach, even the most complex unbalanced scenarios can be broken down into simple, solvable components, making power system analysis much more manageable.
Key Takeaways:
- Symmetrical Components simplify unbalanced three-phase systems.
- They consist of positive, negative, and zero sequence components.
- Used extensively in fault analysis, relay protection, and power quality studies.
- Fundamental for engineers handling symmetrical and asymmetrical power system issues.
Related Articles: