Inductors in series get added because the effective number of turns increases with an increase in total inductance.
In this article, we will learn about Inductors, their connections in series, their mutual inductance, cumulatively coupled series circuits, differentially coupled series circuits, total voltage, and current passing through the circuit.
What is an Inductor?
An inductor is a passive electrical component that stores energy in the form of a magnetic field when a current passes through it. It is made of conducting material having several turns. It is also called a reactor, coil, or choke.
Its value is shown in inductance, which is measured in Henry (H). A large number of turns indicates the large value of the inductor.
Inductors in Series Circuit
We can connect the inductors in series as well as parallel according to requirement. Like resistors and capacitors connections in series, in the same way, we can connect inductors in series. In a series connection, inductors are connected in a chain having the same current because there is only one path for current while the total voltage is equal to the voltage across each inductor. There can be the effect of Mutual inductance, which will increase or decrease the equivalent inductance depending upon the direction of the current of the inductors.
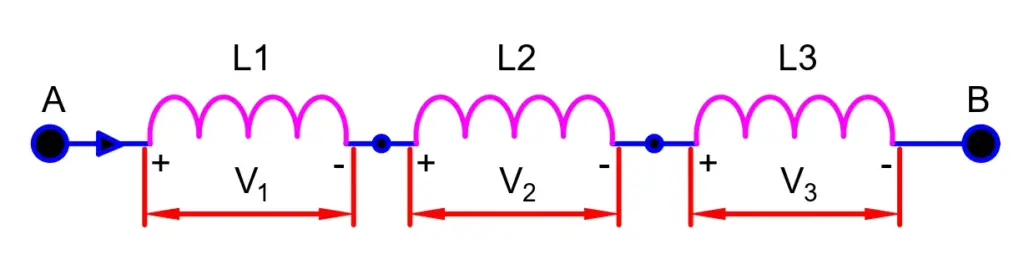
To obtain the equivalent inductance, all the inductors are added like the resistors.
Since the current is continuously changing, a self-inducting process will take place and induced emf will generate across the inductors. Induced emf across 1st Inductor is V1, across 2nd inductor is V2, and across the 3rd inductor is V3.
The total voltage across all the inductors is equal to the sum of the voltage across each inductor.
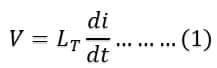
Voltage across 1st Inductor is;
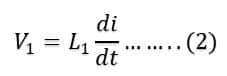
Voltage across 2nd Inductor is;
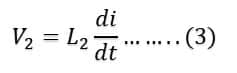
Voltage across 3rd Inductor is;
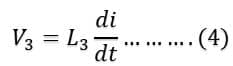
The change of current w.r.t time is the same in each inductor because inductors are connected in series and the same current pass-through the whole branch.
So, we can say that the total voltage is
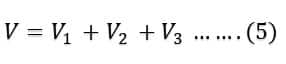
Putting the value of V1, V2 and V3 from equation 3,4 &5 in equation 5, we get;
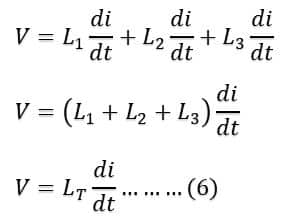
Here, L is the total inductance of the series-connected inductor. Thus, the total inductance of the series-connected inductor is equal to the sum of the individual inductance of the inductor.
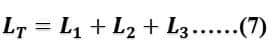
If there are “n” numbers of inductors connected in the series, then the total inductance will be;
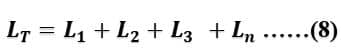
Inductors in series with Mutual Inductance
When the inductors are placed at a distance from each other, magnetic flux will not pass from each other of every inductor, so, there is no mutual inductance and the equivalent inductance will be the same.
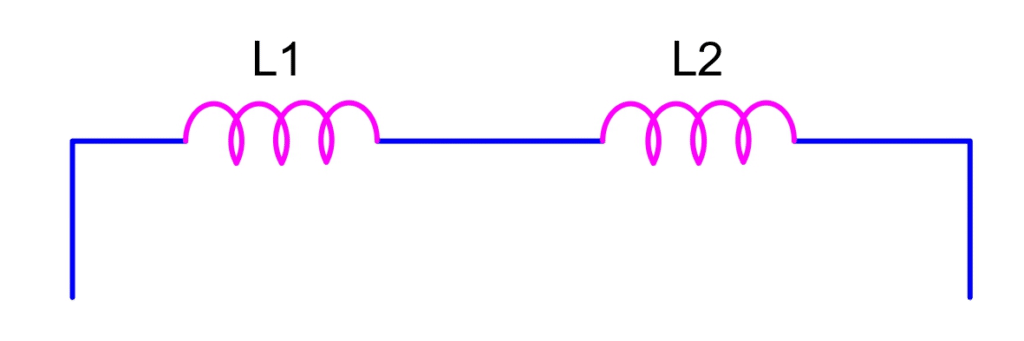
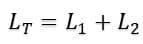
Here, mutual inductance is zero, because, the inductors are placed at a distance and there is no effect on each other.
The behavior of flux linking can be
- Series Aiding Connection
- Series Opposing Connection
If there is a smaller distance between the inductors, then magnetic flux will link with the inductors. This magnetic flux can be in the same direction or the opposite direction.
Cumulatively coupled series circuit / Series Aiding Connection
Since the current is continuously changing, so flux of 1st coil will link with the flux of 2nd coil and the same behavior for the 2nd coil. If the magnetic flux of 1st coil is linked with the flux of 2nd coil in the same direction, then it is called Adding connection of inductors or cumulatively coupled series circuit. It means the entering of current in both coils is the same or the polarity is the same.
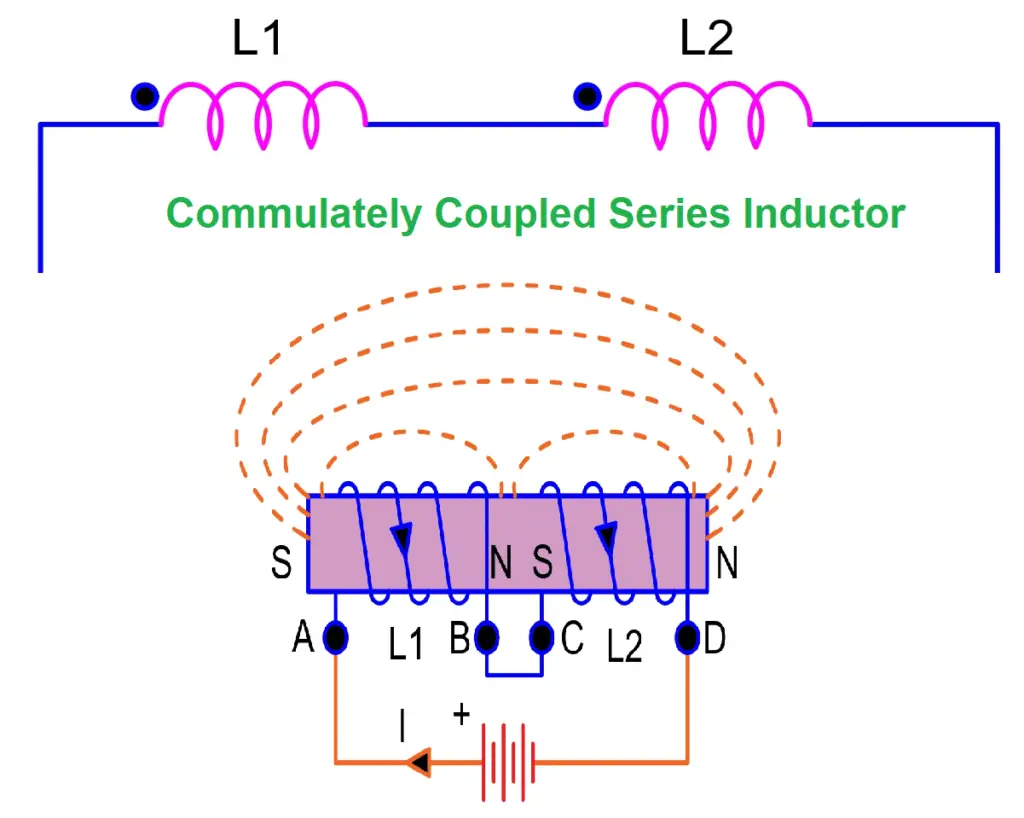
In the above circuit, we can see the direction of current along with the magnetic field is the same in both inductors. So, here M will be added to the self-inductances, which will increase its overall inductance and the equivalent equation will be:
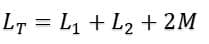
Differentially coupled series circuits / Series Opposing Connection
Since the current is continuously changing, so flux of 1st coil will link with the flux of 2nd coil and the same behavior for the 2nd coil. If the magnetic flux of 1st coil is linked with the flux of 2nd coil in the opposite direction, then it is called the Opposing connection of inductors or differentially coupled series circuits. It means, the entering of current in both coils is different or the polarity is different.
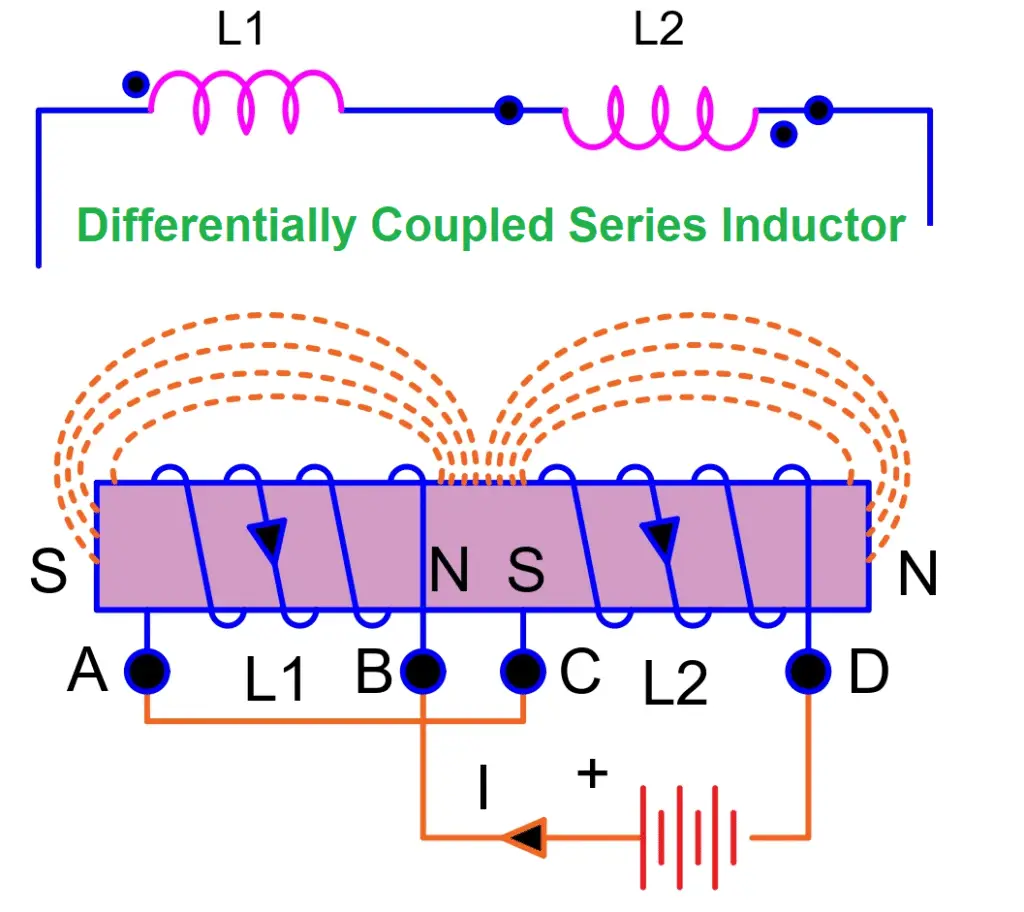
In the above circuit, we can see the direction of current along with the magnetic field is opposite in both inductors. So, here M will be subtracted from the self-inductances, which will decrease the overall inductance and the equivalent equation will be:
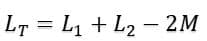
During this mutual inductance phenomenon, any change in one coil will affect the other coil. Factor 2 is multiplied by M; it indicates that the phenomenon of mutual inductance is from both sides.
Example with series inductors (neglecting the Mutual Inductance)
Calculate the total inductance of the series combination, if two inductors of the 70mH and 30mH are connected in series. (Neglect the mutual inductance)
Given Data-
L1 = 70mH
L2 = 30mH
M = 0
We know that,
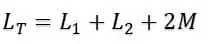
Therefore,
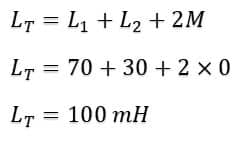
Example with series inductors (Including the Mutual Inductance)
Example-1: two inductors of the 50mH and 60mH are connected in series with a mutual inductance of 6mH, calculate the equivalent inductance of the series combination.
Given Data-
L1 = 50mH
L2 = 60mH
M =6mH
LT = ?
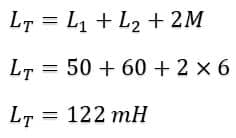
Example-2: Calculate the mutual impedance of series combination, if two inductors are 20mH and 30mH, with the total inductance of the circuit is 70mH are connected in series.
Given data-
L1 = 20mH
L2 = 30mH
LT = 70mH
M= ?
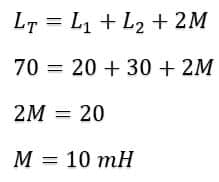
Conclusion
The inductor is a passive electrical component that can store the energy in form of a magnetic field. According to our needs, we can connect it in series, parallel, or series-parallel combinations. In series, inductors are connected in a chain, and total inductance is calculated just like resistors, and all inductances are added.
Current is the same through each inductor because there is only one path and total voltage is equal to the sum of all voltages across the inductors. There can be the effect of mutual inductance while connected in series or parallel.
In a Cumulatively coupled series circuit, the overall inductance will be increased because the magnetic flux of inductors will be linked with each other in the same direction due to the same polarity. On the other hand, in differentially coupled series circuits, the net inductance will be decreased, because the magnetic flux of inductors will be linked with each other in opposite directions due to different polarity.