Definition of Self Induced EMF
Self-induced EMF is the electromagnetic force induced in the coil when the current in a coil or conductor changes. The changing flux when linked to a coil turn, it produces EMF in the coil. Thus, the induced emf in the coil depends upon the rate of change of linked flux.
How Self Induced EMF Occurs
We can understand the induced EMF phenomenon using the below diagram.
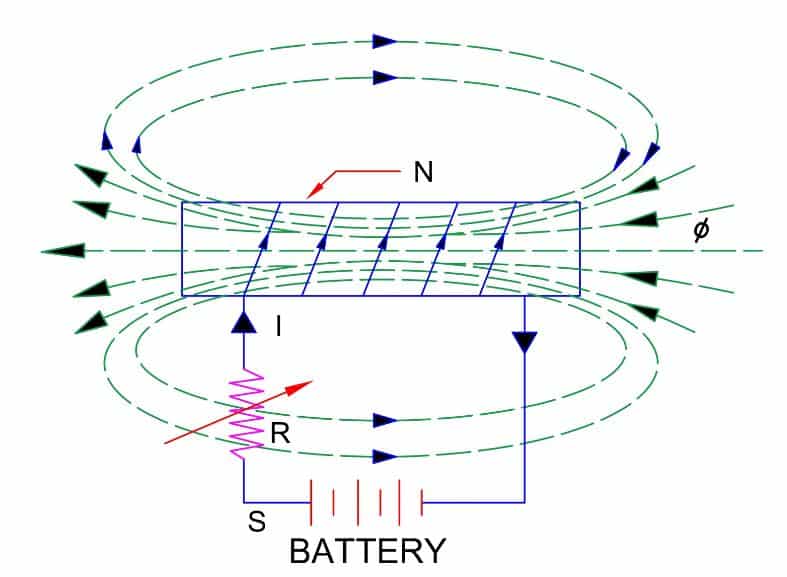
Let the coil has N number of turns. The current I flows through the coil on closing the switch S. The current I produces flux in a coil and further this flux links to the coil’s own turns.
The linking flux produces the EMF in a coil. This EMF is called Self-Induced EMF. The EMF in a coil changes with a change in current flowing through a coil. We can change the magnitude of the current through a coil by changing the resistance of variable resistance(R).
Direction of Self Induced EMF (Lenz’s Law)
The direction of induced EMF always opposes the very own cause which produces it. The change in the current produce EMF, therefore the induced EMF always opposes the current. This happens as per the Lenz’s Law.
Formula of Self-Induced EMF
The induced EMF in a coil is proportional to the rate of change of current in a coil.
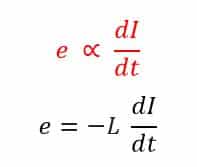
Here negative sign shows that the induced EMF opposes the rate of change in the current. L is the constant of proportionality. It is the Self Inductance of a coil.
Factors Affecting Self Induced EMF
The magnitude of self-induced EMF in a coil depends on several important factors:
- Number of Turns (N) in the Coil
- The more turns a coil has, the greater the magnetic flux linkage, which increases the induced EMF.
- Self-Inductance (L) of the Coil
- A coil with higher self-inductance produces a larger EMF for the same rate of current change. Self-inductance depends on the coil’s geometry and core material.
- Rate of Change of Current (dI/dt)
- The faster the current changes in the coil, the higher the induced EMF. A sudden change in current produces a stronger self-induced EMF.
- Core Material (Air Core vs Iron Core)
- Coils with iron cores produce higher EMF than air-core coils because the magnetic permeability of iron is much greater, resulting in stronger flux linkage.
Applications of Self Induced EMF
Here are some key applications:
- Transformers
- In transformers, self-induced EMF occurs in both the primary and secondary coils, helping regulate voltage and transfer energy efficiently between circuits.
- Inductors in Circuits
- Inductors use self-induced EMF to oppose sudden changes in current, protecting sensitive components and maintaining smooth current flow.
- Electric Motors and Generators
- Self-induced EMF, often called back EMF, helps regulate voltage and current in motors and generators, ensuring stable operation.
- Relays and Solenoids
- When the current through a relay or solenoid coil changes abruptly, self-induced EMF prevents voltage spikes that could damage the circuit or components.
Solved Example of Self Induced EMF
The inductance of a coil is L =8 H and resistance R = 2 Ω. If the applied voltage of the battery is 8 V and it switches off in 1 ms, find induced emf.
Given Data,
L = 8 H
V= 8 Volts
R = 2 Ω
t = 1 ms = 1 X 10-3 s
e = ?
The current through the coil
I = V/R = 8/2 = 4 A
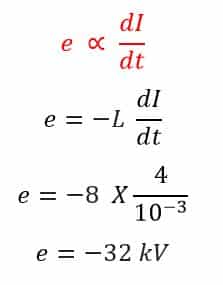
The negative sign shows the direction of emf that opposes the change in flux or the flow of current.
Therefore, e = 32 kV
H2: Key Points to Remember
- Self Induced EMF depends on the rate of change of current.
- Its direction always opposes the change (Lenz’s Law).
- Formula: e=−LdI/dt
Conclusion
Self Induced EMF is a fundamental concept in electromagnetism, representing the EMF generated in a coil due to its own changing current. It always opposes the change in current, as explained by Lenz’s Law, and is directly proportional to the rate of current change through the coil.
Understanding this phenomenon is essential for designing coils, transformers, and inductive circuits in electrical engineering.
Explore the broader concept of Induced EMF, including its types and units, in our detailed guide: Induced EMF: Meaning, Types, and Units.
Related Articles: