In the study of electricity, resistance is one of the most fundamental concepts. It represents how much a material opposes the flow of electric current. Every electrical component, wire, or device has some resistance. Understanding the resistance formula helps in analyzing and designing efficient electrical and electronic systems.
What is Resistance?
Resistance is the property of a material that restricts the movement of electrons through it. It is denoted by R and measured in ohms (Ω).
When current flows through a conductor, collisions occur between electrons and atoms, converting some electrical energy into heat. This opposition to the flow of current is what we call electrical resistance.
Resistance Formula
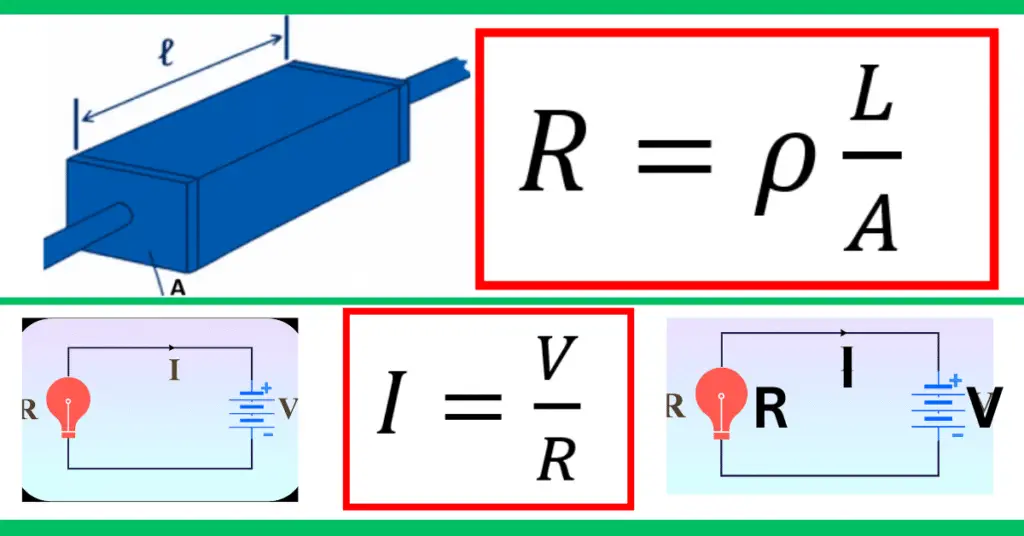
The basic resistance formula is:
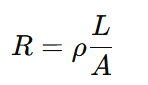
- R = Resistance (ohms, Ω)
- ρ (rho) = Resistivity of the material (ohm-meter, Ω·m)
- L = Length of the conductor (meter, m)
- A = Cross-sectional area of the conductor (square meter, m²)
This equation shows that resistance increases with the length of the conductor and decreases with the increase in cross-sectional area.
Ohm’s Law and Resistance Formula
Ohm’s Law gives the relationship between voltage (V), current (I), and resistance (R): V=I×R
From this, the resistance formula becomes:
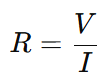
Where:
- V = Voltage across the conductor (volts)
- I = Current flowing through it (amperes)
- R = Resistance (ohms)
This version of the formula is used when voltage and current are known. It connects the electrical behavior of a circuit directly with measurable quantities.
By combining Ohm’s Law (V = IR) and the resistivity-based formula (R = ρL/A), one can understand both the electrical and physical aspects of resistance.
Resistance Formula for Conductors, Insulators, and Semiconductors
Different materials have different resistivity values, which influence their resistance. The resistance formula remains the same, but resistivity (ρ) varies significantly among conductors, insulators, and semiconductors.
1. Resistance Formula for Conductors
Conductors like copper, silver, and aluminum have very low resistivity (ρ ≈ 10⁻⁸ Ω·m).
Hence, their resistance is very small: R=ρL/A
Example:
A copper wire of 2 m length and 1 × 10⁻⁶ m² area gives R ≈ 0.0336 Ω.
Conductors are ideal for carrying current efficiently with minimal losses.
2. Resistance Formula for Insulators
Insulators such as rubber, glass, and plastic have extremely high resistivity (ρ ranges from 10⁸ to 10¹⁶ Ω·m).
Even though the resistance formula (R = ρL/A) is the same, the high resistivity makes their resistance almost infinite.
Example:
If ρ = 10¹⁰ Ω·m, L = 1 m, A = 1 × 10⁻⁶ m²
R=1016Ω
Such materials block electric current almost completely, making them ideal for insulation purposes.
3. Resistance Formula for Semiconductors
Semiconductors like silicon and germanium have moderate resistivity (ρ ≈ 10⁻³ to 10³ Ω·m).
Their resistance is temperature-dependent and decreases as temperature increases, unlike metals. R=ρL/A
For semiconductors, resistivity (ρ) can be controlled by doping — adding small amounts of impurities to improve conductivity.
Hence, semiconductors play a key role in electronic devices, transistors, and integrated circuits.
Example Calculation Using Resistance Formula
Let’s calculate the resistance of a copper wire.
Given:
- Length, L = 2 m
- Area, A = 1 × 10⁻⁶ m²
- Resistivity, ρ = 1.68 × 10⁻⁸ Ω·m
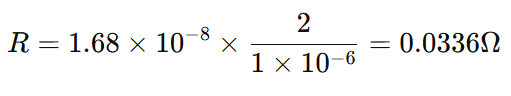
So, the wire’s resistance is 0.0336 Ω.
Resistance Formula for Resistance in Series and Parallel
1. Resistance in Series
When resistors are connected one after another, the total resistance is the sum of all:
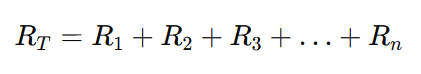
Here, current remains the same, but voltage divides across each resistor.
2. Resistance in Parallel
When resistors are connected across the same voltage source:
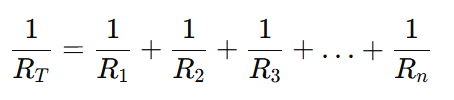
Here, voltage remains the same across each resistor, but current divides depending on resistance.
Factors Affecting Resistance
- Material type – Different materials have different resistivities.
- Temperature – In conductors, resistance increases with temperature, but in semiconductors, it decreases.
- Length (L) – Longer conductors have higher resistance.
- Area (A) – Thicker conductors have lower resistance.
Importance of Resistance Formula in Electrical Engineering
The resistance formula is widely used in electrical and electronic design for:
- Calculating voltage drops in circuits.
- Designing resistors, heaters, and wiring systems.
- Selecting suitable materials based on resistivity.
- Ensuring safety and efficiency by minimizing power loss (P = I²R).
- Studying material behavior across temperature variations.
Applications of Resistance Formula
- Determining the resistance of conductors and components.
- Designing energy-efficient electrical systems.
- Calculating heating effects in electrical devices.
- Testing and characterizing new materials for conductivity.
Conclusion
The resistance formula (R = ρL/A) and Ohm’s Law (V = IR) are the foundations of electrical science. They explain how the resistance of a material depends on its dimensions, resistivity, and electrical properties.
From conductors to insulators and semiconductors, the same resistance formula helps engineers and students understand how current flows differently in various materials. Whether in wiring, electronics, or energy systems, mastering this concept ensures safe, efficient, and reliable circuit design.
Related Articles: